Tree Computations

Required Readings

• Parallel Tree Contraction and its Application
• Course Notes

Optional

• Prof Tvrdik’s Notes
• Prof Tvrdik’s Slides

Summary

• Parallel Root Finder
• Parallel Independent Set
• Seemingly Sequential Tree Algorithm
• Euler Tour Technique
  • How to get post order numbering:
  • Implementing Euler Tours

Parallel Root Finder

Trees can be stored as an array pool, with an array storing the parents.

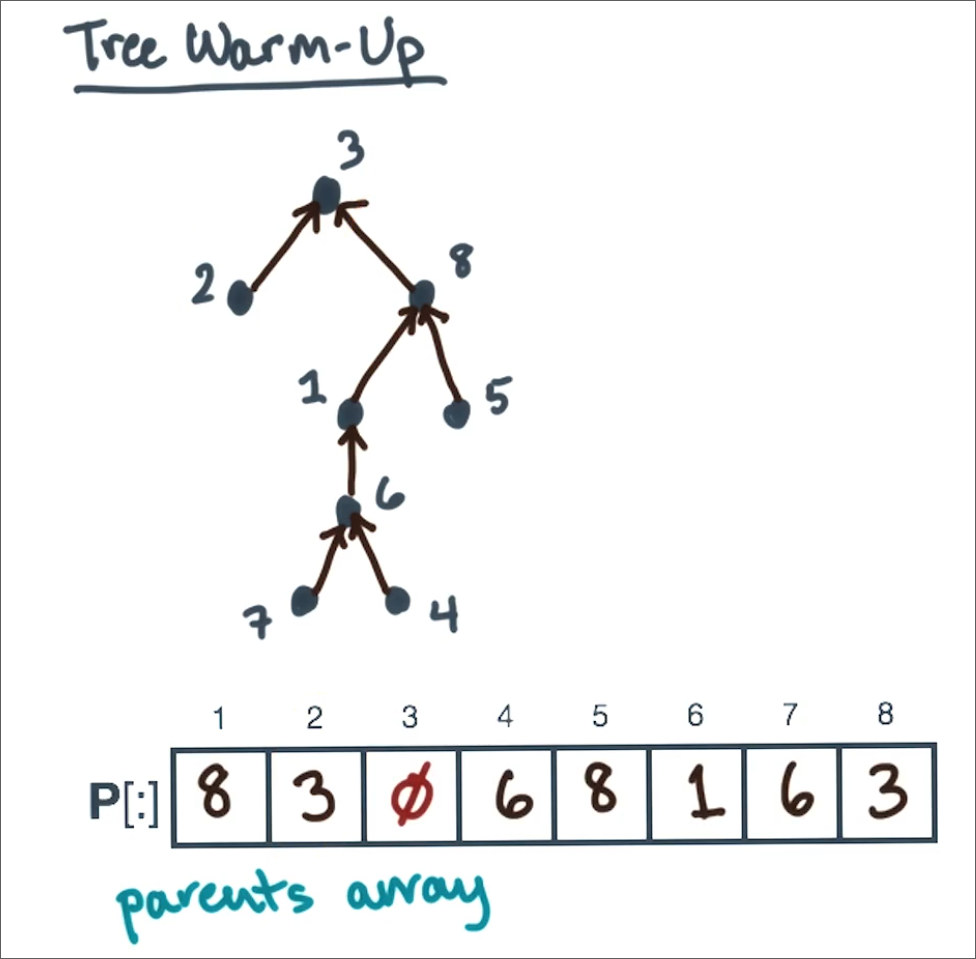
A sequential algorithm to find the root would look like so

root(P[1:n])
  if n < 1 then return 0
  node <- (any node, 1 .. n)
  while P[node] != 0 do
    node <- P[node]
  return node

Runtime = O(n)

A parallel idea is to explore all nodes simultaneously by changing each parent to the grandparent, until there are no more grandparents.

hasGrandparent(k, P[1:n])
  return (k>0) and (P[k]>0) and (P[P[k]] > 0)

adopt(P[1:n], G[1:n])
  par-for i<-1 to n do
    if hasGrandparent(i, P[:])
    then G[i] <- P[P[i]]
    else G[i] <- P[i]

findRoots(P[1:n], R[1:n])
  let P_cur[1:n] <- P[:]
  let P_next[1:n] <- temp_buf
  for l <- 1 to ciel(log(n)) do
    adopt(P_cur[:], P_next[:])
    P_cur[:] <- P_next[:]
  R[:] <- P_cur[:]

Parallel Independent Set

If you want to shrink a list, a good tool is the Parallel Independent Set (PIS).

Independent Set
Given a list, a set I of vertices such that every element in the set does not have its successor in the set. $$i \in I \implies N[i] \notin I$$

Sequentially, you can just start at the head and add every other node to the set.

To compute it in parallel, you need to break the symmetry (all nodes lookging the same).

1. Flip a coin. If tails, the node is NOT in the set. If heads, the node is a candidate for the set.
2. If a candidate’s successor is a candidate, the predecessor is not a candidate.
3. Collect all remaining candidates.

ParIndSet(N[1:n], I[:])
  let C[1:n], C'[1:n] <- space for coins
  par-for i <- 1 to n do
    C[i] <- flipCoin(H/T) // rand(0..1) > 0.5
    C'[i] <- C[i] // make a copy
  par-for i <- 1 to n do
    // If I'm heads, and I have a successor, and the successor is heads, I am
    // tails.
    if (C'[i] = H) and (N[i]>0) and (C'[N[i]] = H) then
      C[i] <- T
  I[:] <- gatherIf(1:n, C[1:n])

Work = W(n) = O(n)

Span = D(n) = O(log(n))

On average, 1/4 nodes end up in the IS

For work optimal List Scanning, use PIS to determine the heads of Wyllie’s and/or Helmann-JaJa

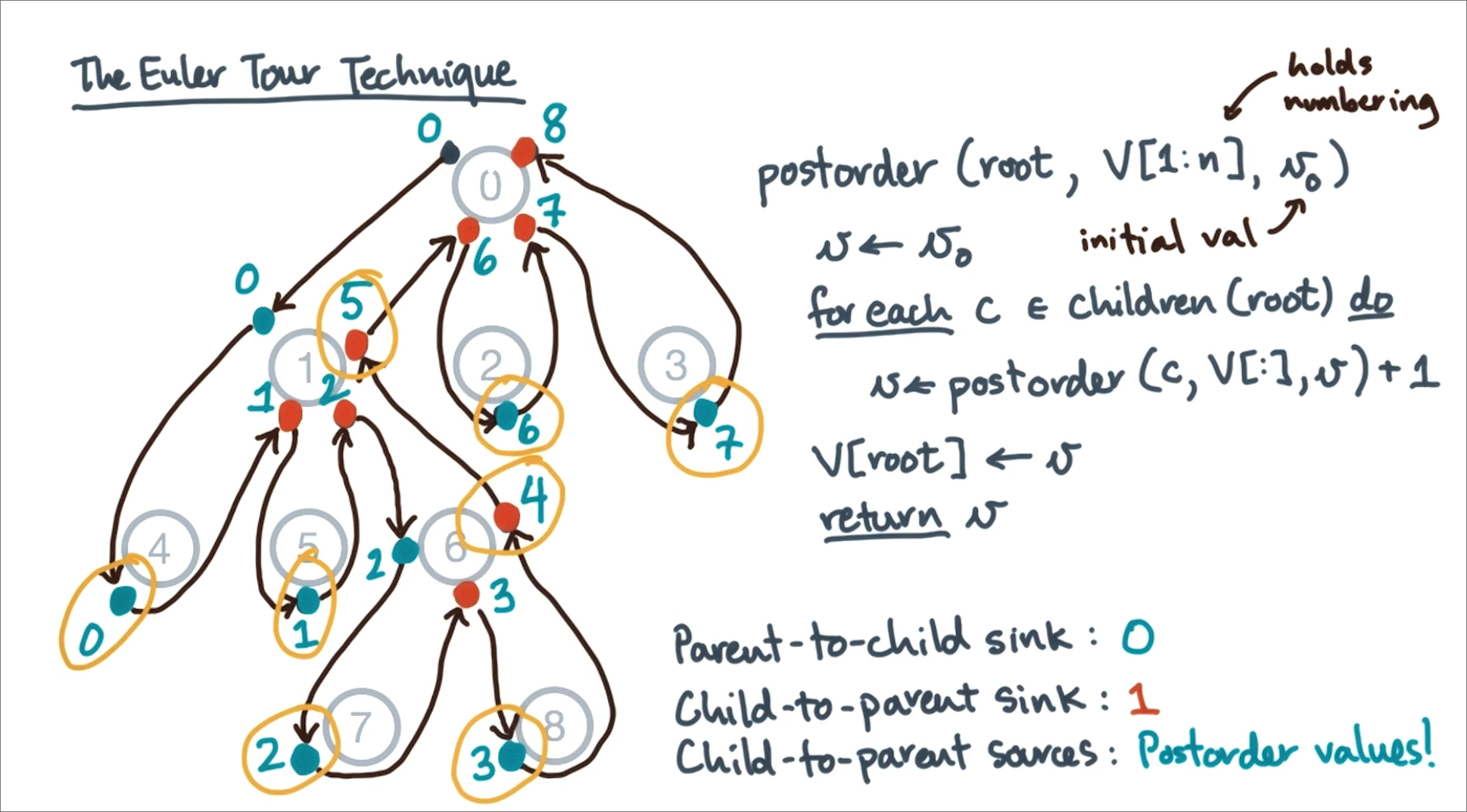
Seemingly Sequential Tree Algorithm

// Root, numbering, initial value
postOrder(root, V[1:n], v_0)
  v <- v_0
  for-each c in children(root) do
    v <- postOrder(c, V[:], v) + 1
  V[root] <- v
  return v

Euler Tour Technique

Take a tree, change every bidirectional edge to two unidirectional edges. Now we get a directed circuit. This circuit gives you a linked list.

Directed Circuit
A closed path that uses every edge exactly once.

How to get post order numbering:

• Set parent-to-child sink: 0
• Set child-to-parent sink: 1
• Do a scan
• child-to-parent sources now equal post order numbering!

Implementing Euler Tours

You need a graph to get from node to node

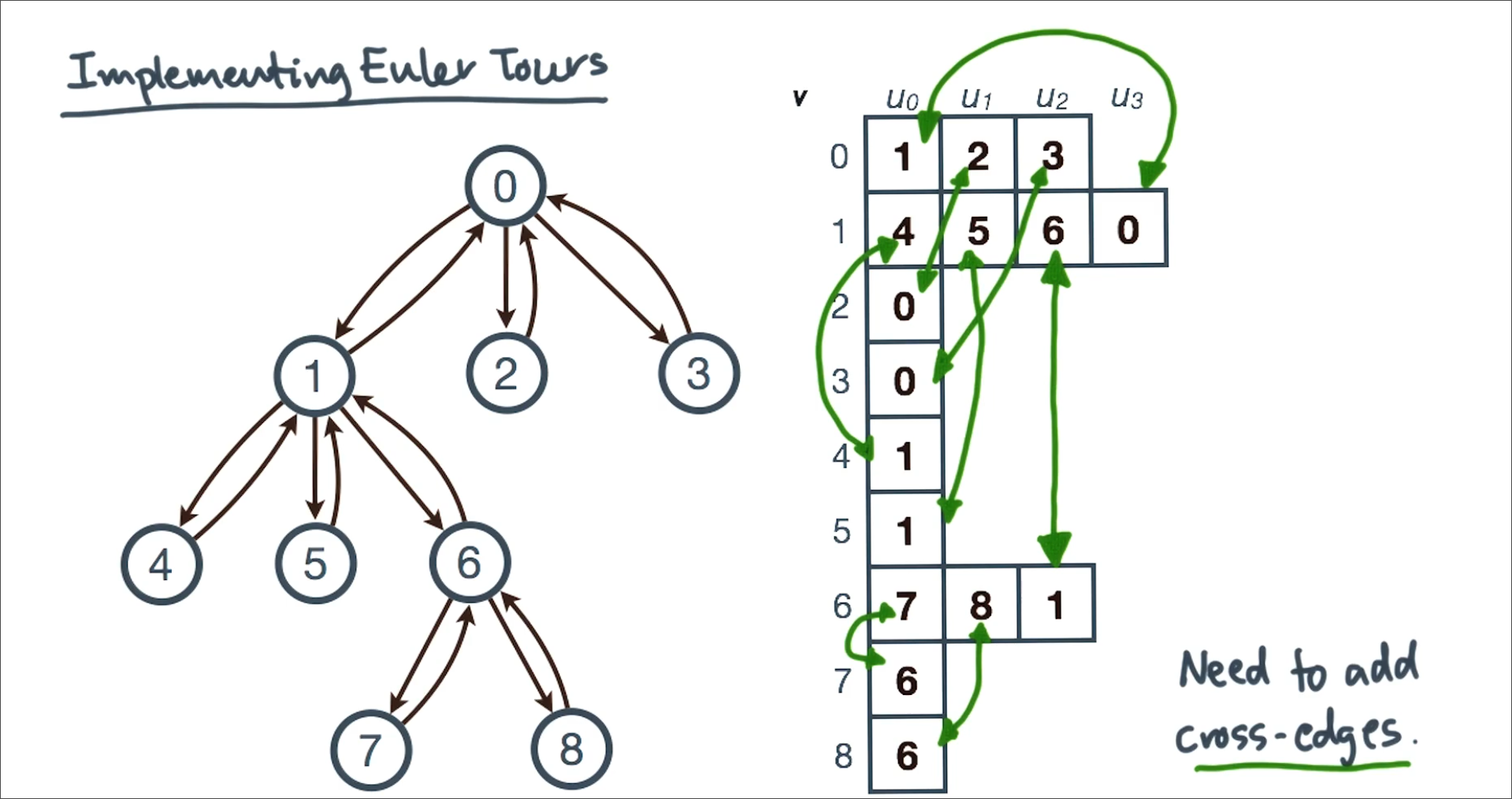
Also, the successor function: $s(u_i,v) \equiv (v, u_{(i+1)\mod d_v})$